If an amount
A is left in an account at interest r, the total value V
- after 1 year, V[1] = (1+r) A
- after 2 year, V[2] = (1+r) V[1] = (1+r)2 A
- after n year, V[n] = (1+r)n A
Sometime, we describe compound on monthly basis. For example, your mortgage interest is quoted as annual interest, but you pay monthly
- on monthly basis, after n year, V[n] = (1+r/12)n*12 A
Interest rate is important to determine the value of a cash flow. For example, if you happen to win a lottery, you will have two options :
(1) you can choose to get one lump sum
(2) you can get annual payment for, say, 26 years.
In terms of cash flow, it looks like this
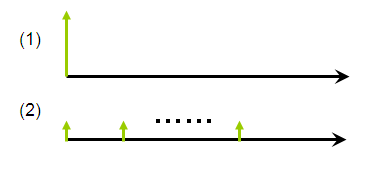
So, which one makes sense to you, and why ? To understand this, we need to use the next concept which is Net Present Value (NPV).

